Quantitative image analysis#

After segmenting and labeling objects in an image, we can measure properties of these objects.

See also

Before we can do measurements, we need an image and a corresponding label_image. Therefore, we recapitulate filtering, thresholding and labeling:

from skimage.io import imread
from skimage import filters
from skimage import measure
from pyclesperanto_prototype import imshow
import pandas as pd 
import numpy as np

# load image
image = imread("../../data/blobs.tif")

# denoising
blurred_image = filters.gaussian(image, sigma=1)

# binarization
threshold = filters.threshold_otsu(blurred_image)
thresholded_image = blurred_image >= threshold

# labeling
label_image = measure.label(thresholded_image)

# visualization
imshow(label_image, labels=True)
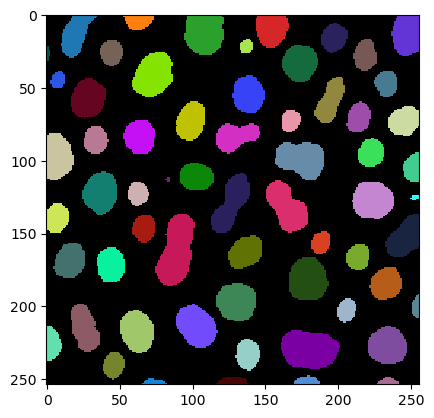
../_images/5257573298d6a444b6a34d09506d6cf9a10aab208bce52c927a91ea6491b20ee.png

Measurements / region properties#

To read out properties from regions, we use the regionprops function:

# analyse objects
properties = measure.regionprops(label_image, intensity_image=image)

The results are stored as RegionProps objects, which are not very informative:

properties[0:5]

[<skimage.measure._regionprops.RegionProperties at 0x1c272b8f8e0>,
 <skimage.measure._regionprops.RegionProperties at 0x1c26d278af0>,
 <skimage.measure._regionprops.RegionProperties at 0x1c26d2784c0>,
 <skimage.measure._regionprops.RegionProperties at 0x1c26d278b20>,
 <skimage.measure._regionprops.RegionProperties at 0x1c26d278b80>]

If you are interested which properties we measured: They are listed in the documentation of the measure.regionprops function. Basically, we now have a variable properties which contains 40 different features. But we are only interested in a small subset of them.

Therefore, we can reorganize the measurements into a dictionary containing arrays with our features of interest:

statistics = {
    'area':       [p.area               for p in properties],
    'mean':       [p.mean_intensity     for p in properties],
    'major_axis': [p.major_axis_length  for p in properties],
    'minor_axis': [p.minor_axis_length for p in properties]
}

Reading those dictionaries of arrays is not very convenient. For that we introduce pandas DataFrames which are commonly used by data scientists. “DataFrames” is just another term for “tables” used in Python.

df = pd.DataFrame(statistics)
df
area mean major_axis minor_axis
0 429 191.440559 34.779230 16.654732
1 183 179.846995 20.950530 11.755645
2 658 205.604863 30.198484 28.282790
3 433 217.515012 24.508791 23.079220
4 472 213.033898 31.084766 19.681190
... ... ... ... ...
57 213 184.525822 18.753879 14.468993
58 79 184.810127 18.287489 5.762488
59 88 182.727273 21.673692 5.389867
60 52 189.538462 14.335104 5.047883
61 48 173.833333 16.925660 3.831678

62 rows × 4 columns

You can also add custom columns by computing your own metric, for example the aspect_ratio:

df['aspect_ratio'] = [p.major_axis_length / p.minor_axis_length for p in properties]
df
area mean major_axis minor_axis aspect_ratio
0 429 191.440559 34.779230 16.654732 2.088249
1 183 179.846995 20.950530 11.755645 1.782168
2 658 205.604863 30.198484 28.282790 1.067734
3 433 217.515012 24.508791 23.079220 1.061942
4 472 213.033898 31.084766 19.681190 1.579415
... ... ... ... ... ...
57 213 184.525822 18.753879 14.468993 1.296143
58 79 184.810127 18.287489 5.762488 3.173540
59 88 182.727273 21.673692 5.389867 4.021193
60 52 189.538462 14.335104 5.047883 2.839825
61 48 173.833333 16.925660 3.831678 4.417297

62 rows × 5 columns

Those dataframes can be saved to disk conveniently:

df.to_csv("blobs_analysis.csv")

Furthermore, one can measure properties from our statistics table using numpy. For example the mean area:

# measure mean area
np.mean(df['area'])

355.3709677419355

Exercises#

Analyse the loaded blobs image.

  • How many objects are in it?

  • How large is the largest object?

  • What are mean and standard deviation of the image?

  • What are mean and standard deviation of the area of the segmented objects?