Neighbor meshes in three dimensions

The neighbor meshes we worked with in this chapter in general also work in three dimensions. It is just more challenging to visualize those.

from skimage.io import imread
import pyclesperanto_prototype as cle
import matplotlib.pyplot as plt

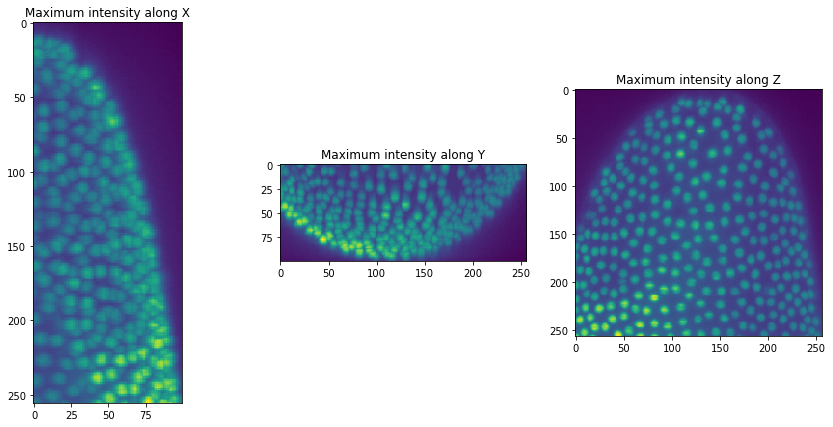
The image data we use here shows a crop of a developing Tribolium castaneum embryo imaged using light sheet microscopy by Daniela Vorkel, Myers lab, MPI-CBG / CSBD Dresden.

raw_image = imread("../../data/Lund_000500_resampled-cropped.tif")

raw_image.shape

(100, 256, 256)

For the ease-of-use we write a short function for visualizing our image stack in three maximum projections from different persepctives.

def orthogonal_show(image, labels=False):

    fig, axs = plt.subplots(1, 3, figsize=(15, 7))

    cle.imshow(cle.maximum_x_projection(image), plot=axs[0], labels=labels)
    cle.imshow(cle.maximum_y_projection(image), plot=axs[1], labels=labels)
    cle.imshow(cle.maximum_z_projection(image), plot=axs[2], labels=labels)
    
    axs[0].set_title("Maximum intensity along X")
    axs[1].set_title("Maximum intensity along Y")
    axs[2].set_title("Maximum intensity along Z")

orthogonal_show(raw_image)

We can now segment nuclei in our our dataset.

background_subtracted = cle.top_hat_box(raw_image, radius_x=5, radius_y=5, radius_z=5)

nuclei = cle.voronoi_otsu_labeling(background_subtracted)

orthogonal_show(nuclei, labels=True)

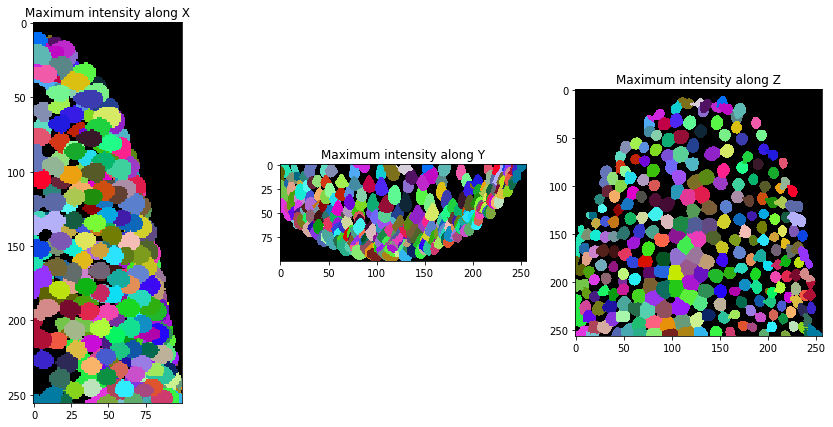
After segmentation, we expand the labels a bit so they touch.

expanded_nuclei = cle.dilate_labels(nuclei, radius=4)

orthogonal_show(expanded_nuclei, labels=True)

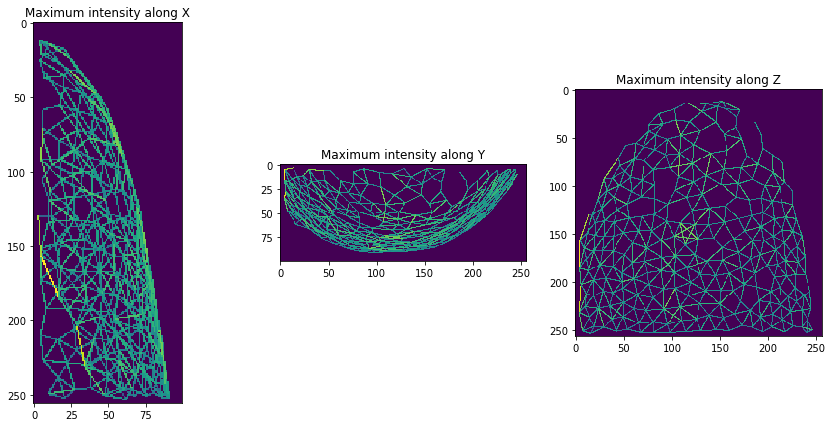
And then, we can visualize a (centroid) distance mesh between touching neighbors.

mesh = cle.draw_distance_mesh_between_touching_labels(expanded_nuclei)

orthogonal_show(mesh)