Filtering images

Image filters take an image and produce a new image. Typically, a filter kernel goes from pixel to pixel and computes a new pixel value depending on an old pixel and its neighborhood.

See also

• Filters in scikit-image

We start with a test image and apply a Gaussian blur filter.

import numpy as np
from pyclesperanto_prototype import imshow
from skimage.filters import gaussian
from skimage import filters
import matplotlib.pyplot as plt
from skimage.morphology import disk
from skimage.io import imread

test_image = np.zeros((10,10))
test_image[5,3] = 1
test_image[5,7] = 1
test_image

array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])

imshow(test_image)

The Gaussian filter takes two important arguments, the image to blur and a sigma parameter. The sigma determines how wide the Gaussian blur should show effects.

blurred = gaussian(test_image, sigma=1)
imshow(blurred)

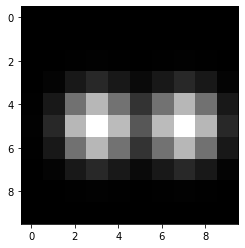
Let’s compare Gaussian blurred images with different sigma

blurred05 = gaussian(test_image, sigma=0.5)
blurred1 = gaussian(test_image, sigma=1)
blurred2 = gaussian(test_image, sigma=2)
blurred3 = gaussian(test_image, sigma=3)

fig, axs = plt.subplots(1, 4, figsize=(15,15))

imshow(blurred05, plot=axs[0])
imshow(blurred1, plot=axs[1])
imshow(blurred2, plot=axs[2])
imshow(blurred3, plot=axs[3])

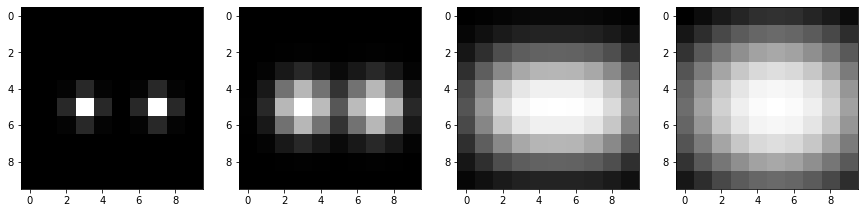
Note: If the sigma is larger than the distance between two spots, the spots cannot be differentiated as two local maxima in the blurred image anymore.